#6 - Calculating the distance between hexagonal tiles

By Hugo on 2024-01-14

Game Development

Tutorial

If you ever took a glance at one of my previous articles, you have noticed that my current work in progress is a tile-based game. More especially, a hexagonal tile-based game. As one can expect, a few days ago I needed a way to calculate the distance between two tiles. If you happen to struggle with this, this article will help you.

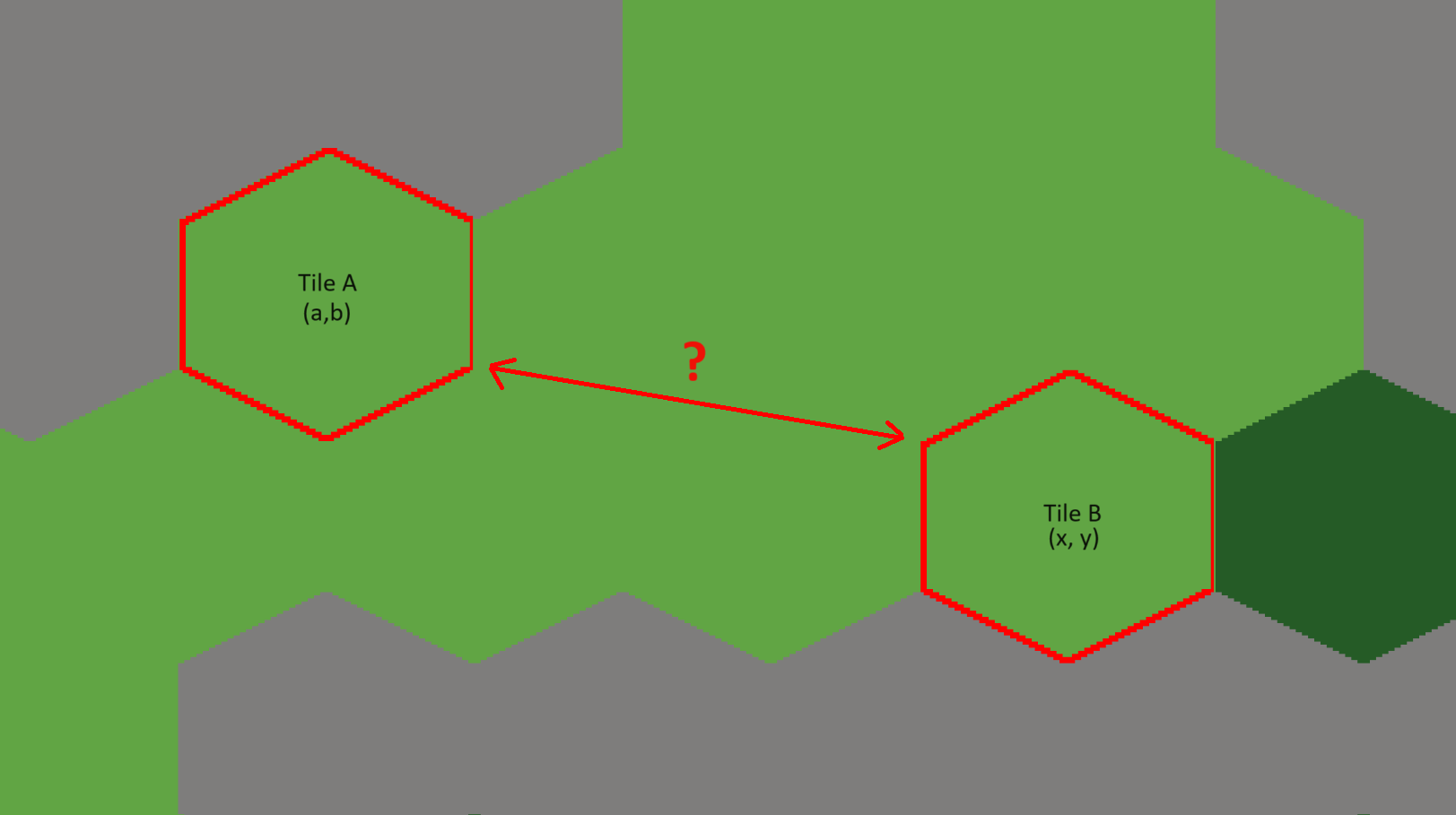
Let’s establish some variables we will use later. Here are our two tiles with their respective coordinates:
Tile A : (a, b)
Tile B : (x, y)

And we want to find the distance between A and B?

A screenshot of my game showing two highlighted tiles with coordinates and the distance between the two

First off, What type of distance?

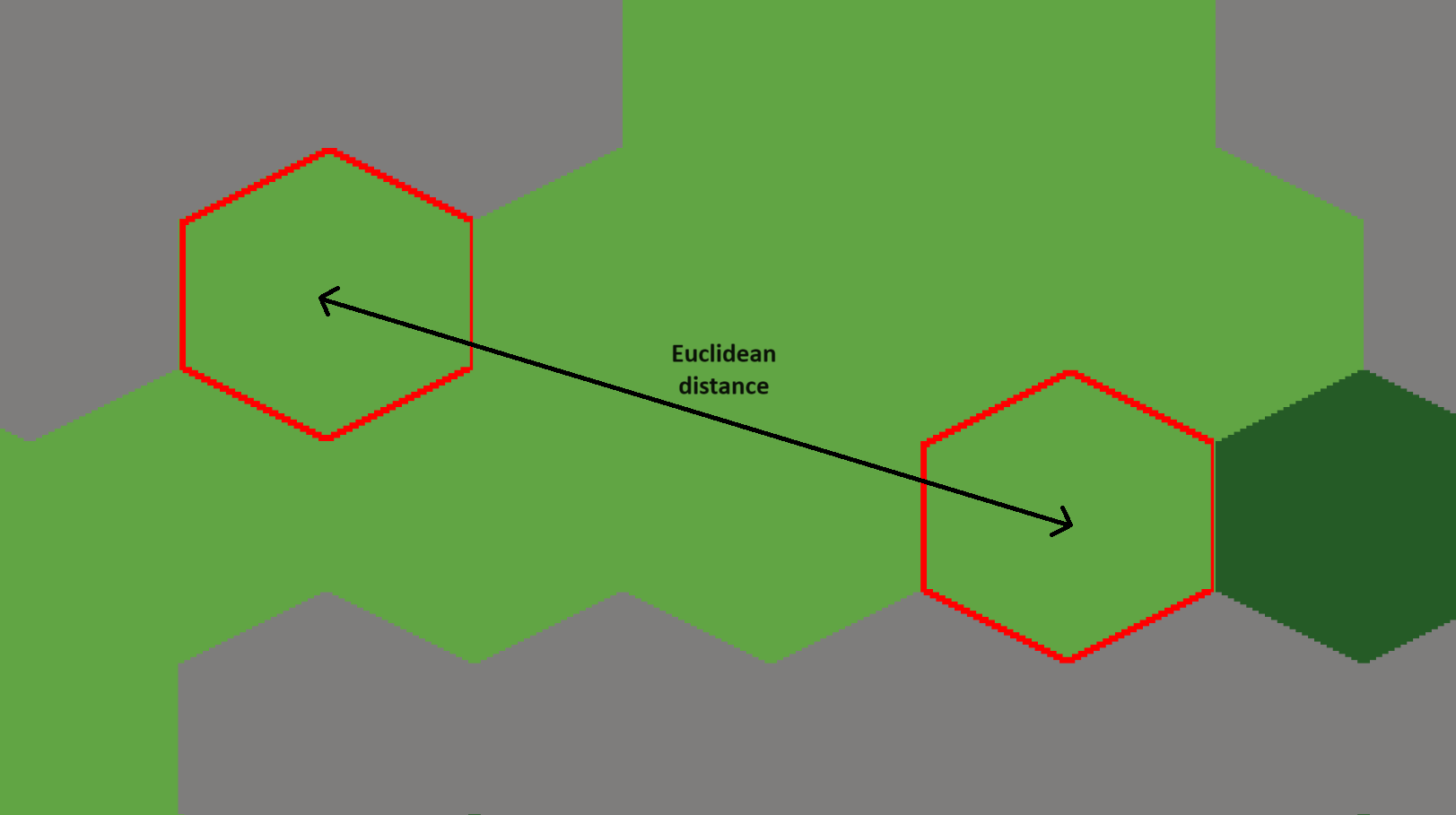
The first step is to establish which kind of distance we need. For those who don’t know, there are many different ways to compute a distance. Most commonly, the term “distance” refers to the Euclidean distance: a straight line from A to B. In a Cartesian coordinate system -exactly what you think a coordinate system is- the Euclidean distance is computed using the Pythagorean theorem.

The formula of the Euclidean distance : D=sqrt((x-a²)+(y-b)²)

A screenshot of my game showing two highlighted tiles and the Euclidean distance between the two

Let's take the following coordinates for a quick test:
Tile A : (0, 0)
Tile B : (2, -1)
Then we expect a distance similar to The numerical application of the previous formula which gives the square root of five.

However, I will eventually implement a pathfinding algorithm and have some troops move from one tile to another. So I want to have integer distances to make the calculations easier.

A screenshot of my game showing two highlighted tiles with numbers on the tiles in between. — In this case we should expect to get a distance of 3, maybe 4 if we count the starting cell.

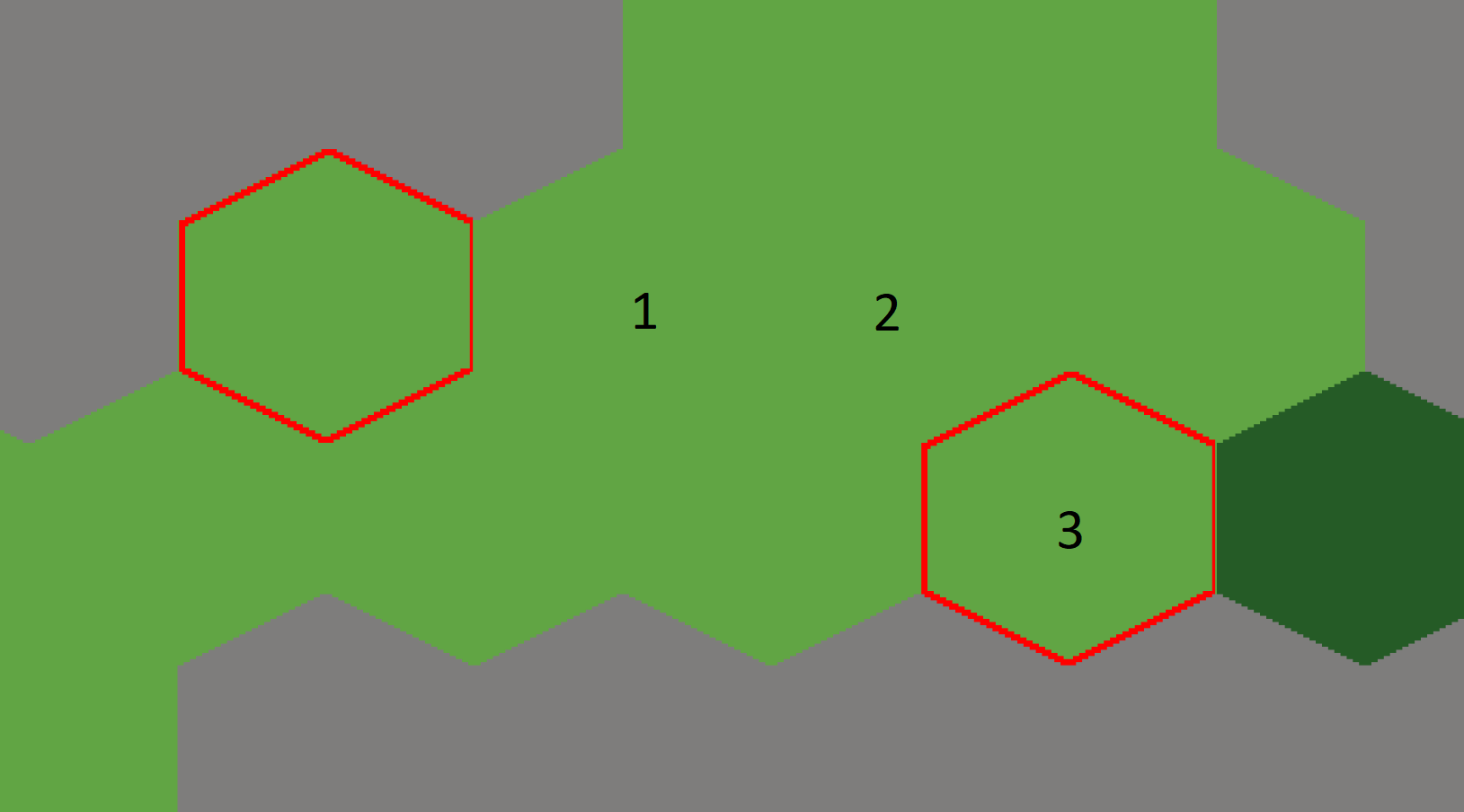
Then, a distance that could work for me could be the Manhattan distance. This one is way easier than the Euclidean distance: the distance is the sum of the distances along the two axes. It is named after the Manhattan island due to the grid-like street layout that force people to travel either horizontally or vertically.

The formula of the Manhattan distance : D=abs(a-x)+abs(b-y)

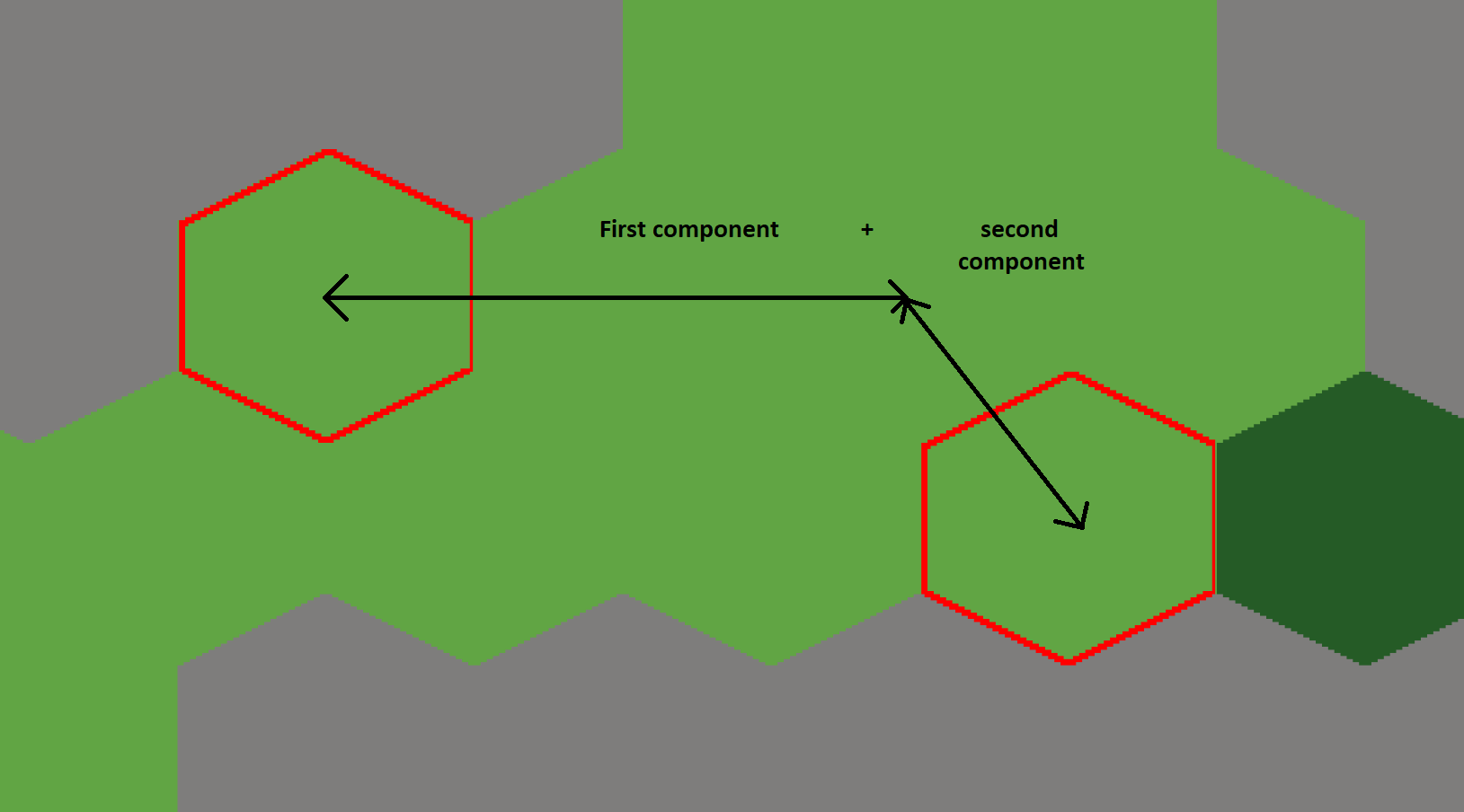
A screenshot of my game showing two highlighted tiles and the Manhattan distance between the two

This distance has the advantage that it returns an integer number which is essentially a tile amount.

What coordinate system?

Representation of the four configuration for the two-dimensionnal hexagonal coordinate system — The types of hexagonal tiling as presented by Red Blob Games

Once again we are faced with multiple options...
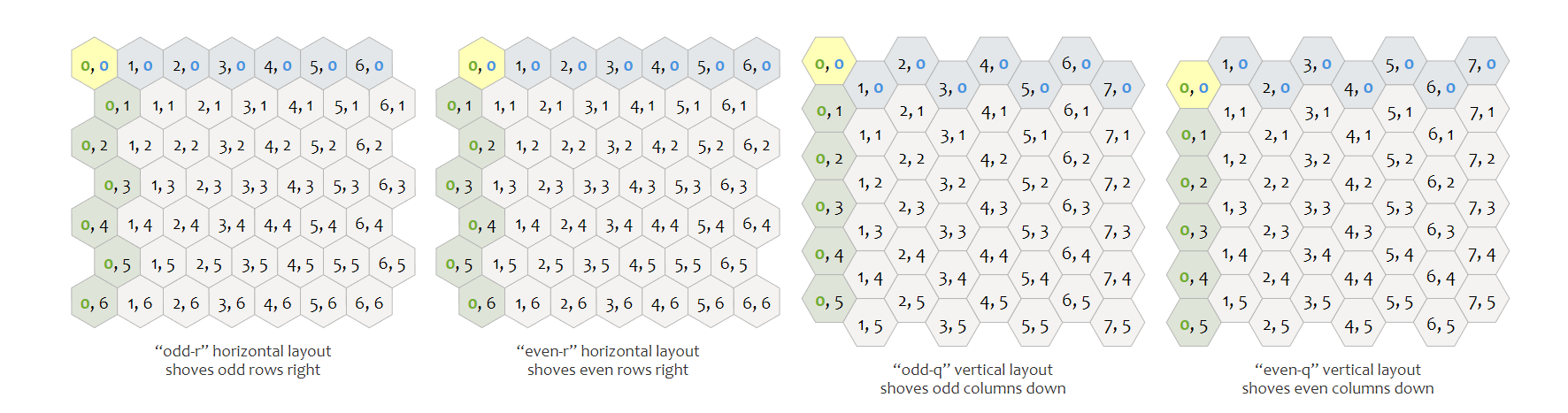
If only there was only one universal truth ! Well, in my situation I am not very far from having a single solution: by not thinking ahead at the start of the project, I am now stuck with an “odd-r” coordinate system (odd lines are offset to the right).

Time to do maths !

Dead simple solution - a basic Manhattan distance

The best way to do things is usually to remain dead simple at first. Then let’s try to compute the Manhattan distance the way we do on a square grid. Spoilers: it was shit…

How to test the efficiency of the solution?

After implementing the first solution, I need a way to test it. I could have written unit tests but nothing could bore me more. On the contrary, I found a nifty little way to visualize my distance: setting different tiles depending on the distance. Let's say, from the center tile:

all tiles at a distance of 1 are painted in dark green
all tiles at a distance of 2 are painted in grey
all tiles at a distance of 3 are painted in light green
all tiles at a distance of 4 are painted in dark green
and so it goes on...

And just like that, we can expect to see concentric cercles appear if the formula is correct.

public static int GetTileDistance(Vector2Int from, Vector2Int to)  {
    return ((int) Mathf.Abs(from.x - to.x) + (int) Mathf.Abs(from.y - to.y));
}

A screenshot of my game showing a tile pattern which does not correspond to the expected concentric circles. Rather, we have a consistent tiling of chunks of two similar tiles. — My first solution is a basic Manhattan distance.

And indeed, as expected, the dead simple solution is trash. I cannot observe anything from the pattern that I created so this formula will most likely not suit my purposes.

Second solution - the horizontal offset

public static int GetTileDistance(Vector2Int from, Vector2Int to) {
  int dx = from.x - to.x; // signed deltas
  int dy = from.y - to.y;
  int x = Mathf.Abs(dx);  // absolute deltas
  int y = Mathf.Abs(dy);
  if ((dx < 0) ^ ((from.y & 1) == 1))
      x = Mathf.Max(0, x - (y + 1) / 2);
  else
      x = Mathf.Max(0, x - (y) / 2);
  return x + y;
}

A screenshot of my game showing a tile pattern which does not correspond to the expected concentric circles. For tiles above and below the center, we start to see straight lines appear in the pattern. For tiles left and right of the center, we see the previous pattern. — Better on the y axis but not exactly that...

My second solution is an attempt at taking into account the y-axis offset of the odd-r configuration. We can see improvement for tiles in the areas above and below the center tile. Having these straight horizontal lines tells me that if I go down or up along a diagonal my distance will increase from 1 to 2 to 3 and so on.

Third and last solution

public static int GetTileDistance(Vector2Int from, Vector2Int to) {
  int offset = ((from.y % 2 == 0 && to.y % 2 == 1 && from.x < to.x) || (to.y % 2 == 0 && from.y % 2 == 1 && to.x < from.x)) ? 1 : 0;
  return Mathf.Max(y,  x + (int)Mathf.Floor(y / 2) + offset);
}

Here, the offset variable describes a vertical offset for tiles that are on a different lines and on different columns.

A screenshot of my game showing a tile pattern of concentric circles. — And here we got concentric circles. It is exactly what I am looking for!

Now, we these concentric circles, I am sure that no matter the direction we go towards, the distance from the starting cell will always be incremented by one after we moved over a tile.

An anecdote to conclude

For the anecdote, I love this kind of clever and quick testing/prototyping. During my internship, I was working on a large MMORPG and was tasked to get familiar with the item effects system. But item effects are massive, they manage everything from giving stats when equipped to triggering specific quest steps.

Because there was no documentation whatsoever on which effect IDs I needed, I solved the struggle in a dumb way: I created a loop that would iterate over all IDs from 0 to 10,000. For each id, I would give myself a placeholder item with the effect applied and with a quantity equal to the id. All there was left to do was go through my stacks of items, find the effects I needed and get their ids from the quantity of this item. However, that forced my server to generate 50,000,000 items and was unresponsive for a while 😃.

I like this anecdote, I hope you did as well ❤️

Thank you for reading to the end! I hope to see you in the next post. 🦦