While working on Void Builder, I encountered a pathfinding problem and if you have read my previous article you know I have a thing for pathfinding. So here goes: my monsters spawn randomly at a given range of the tiles and those monsters must reach the center to attack the beacon.
It looks easy, no? I have a starting position, a destination, discrete positions on a grid and we need to get the list of tiles to cross to reach the destination. We could go for a simple A* pathfinding which Godot already implements.
WRONG! When using A*, monsters prioritize given directions. This means that if a monster is on the diagonal to its destinaton relative to the grid, it will first go vertically then horizontally for example. As a result, all monsters agglomerate on the four directions and that renders most other tiles useless.
This is usable but it does not work for Void builder. The aim of the game is to defend your beacon by placing tiles everywhere. If some paths are prioritized by monsters this completely changes the dynamic of the game and some parts of the map could entirely be defenseless as monsters would rarely walk over them.
Ideally, monsters should go to the center in a straight line.
Would you believe it, an algorithm made to solve this exact issue already exist. I present to you Bresenham's line algorithm!
Given two points, this algorithm returns a list of grid coordinates corresponding to all cells crossed by the resulting line. In short, this algorithm discretize a line relative to a grid coordinate system.
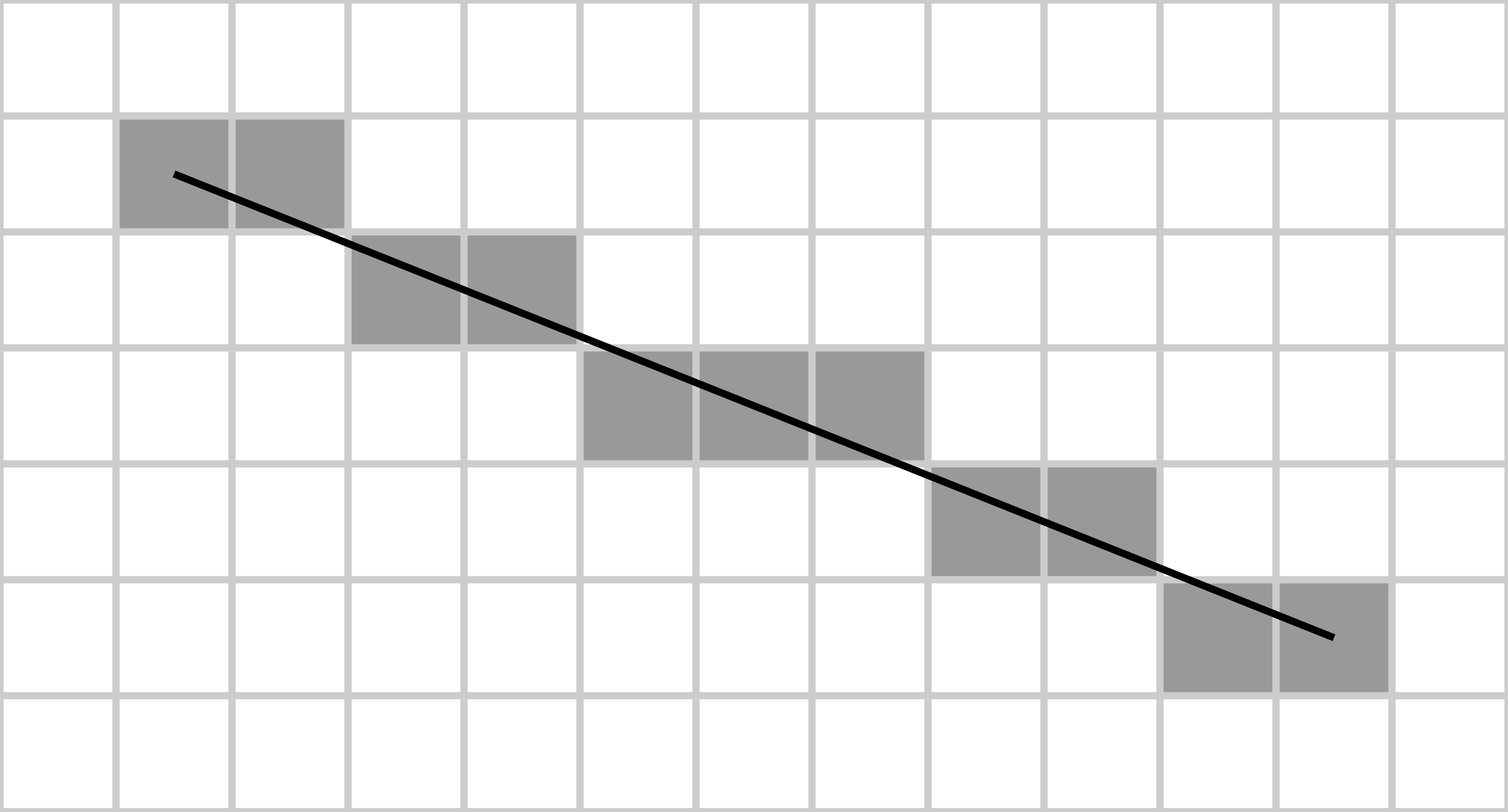
This will allow us to get a direct path from the monster positions to the center of the world that looks intuitive and that suits the game mechanics.
Here is my implementation of it in Godot, let's go over it step by step.
Sea Otter Games1# Bresenham line algorithm
2func get_line_cells(start: Vector2i, end: Vector2i) -> Array[Vector2i]:
3 var cells: Array[Vector2i] = [];
4 var x0 = start.x;
5 var y0 = start.y;
6 var x1 = end.x;
7 var y1 = end.y;
8
9 var dx = abs(x1 - x0);
10 var dy = -abs(y1 - y0);
11 var sx = 1 if x0 < x1 else -1;
12 var sy = 1 if y0 < y1 else -1;
13 var err = dx + dy; # error term
14
15 while true:
16 cells.append(Vector2i(x0, y0));
17 if x0 == x1 and y0 == y1:
18 break;
19 var e2 = 2 * err;
20 if e2 >= dy:
21 err += dy;
22 x0 += sx;
23 continue;
24 if e2 <= dx:
25 err += dx;
26 y0 += sy;
27 continue;
28 return cellsAs expected, the algorithm takes in two points to describe a line and outputs an array containing the coordinates of each crossed cells. In the first few lines, we simply store the components of the starting and ending points. We do this both for comfort and because we will use some compnents to increment the step at which we evaluate the line value.
1func get_line_cells(start: Vector2i, end: Vector2i) -> Array[Vector2i]:
2var cells: Array[Vector2i] = [];
3var x0 = start.x;
4var y0 = start.y;
5var x1 = end.x;
6var y1 = end.y;Then we define some useful variables. The dx and dy variables are respectively the horizontal and vertical distances to the ending point. The sx and sy variables describe the steps with which we travel the line horizontally and vertically. If sx is positive we go from left to right and if sy is positive we go up. In this case, we increment by one in either directions but you could use more if working in world coordinates rather than grid coordinates.
Finaly, err describes the error term. It is the distance between the evaluated point and the actual value on the line. We will not reset this value during the process but simply adjust it:
💡 Warning: The vertical direction can vary according to the coordinate system of your game engine. Here we use the convention of a regular graph meaning y increases as we go up.
Note that dy is negative, we will get back to it later on.
1var dx = abs(x1 - x0);
2var dy = -abs(y1 - y0);
3var sx = 1 if x0 < x1 else -1;
4var sy = 1 if y0 < y1 else -1;
5var err = dx + dy; # error termNow we need to focus on the core of the algorithm. The loop starts is straightforward:
1cells.append(Vector2i(x0, y0));
2 if x0 == x1 and y0 == y1:
3 break;
4 var e2 = 2 * err;
5 ...
6return cellsKeep in mind that dy is negative. So a low or negative error term means the error increases vertically and conversely.
And now we branch between two possibilities:
e2 >= dy - we are vertically close to the line) and we step horizontally (x0 += sx) to get closer to the line.e2 <= dx - we are vertically far from the line) and we allow ourselves to take a vertical step (y0 += sy).And in each case, we increase the error term accordingly. If we stepped horizontally, we grew further from the line vertically and must increase the vertical error.
1if e2 >= dy:
2 err += dy;
3 x0 += sx;
4 continue;
5if e2 <= dx:
6 err += dx;
7 y0 += sy;
8 continue;This algorithm is powerful because it only deals with integers and completely skips computing the line's slope. While this is most often an obsolete consideration this may prove relevant in situations where perfomance is critical.
Finaly, I will conclude by mentionning that my explanation is barely a comprehensive overview of one implementation of the algorithm. Some parts are still hard to intuit for me. If you wish to go deeper into the subject, I suggest watching NoBS Code's video on the subject. They study another implementation of the algorithm but you will find similarities and understand the shortcuts that are necessary to reach such a streamlined algorithm.
Hopefully you appreciate this kind of technical articles and I hope to see you in the next post. 🦦