If you have read some of my previous articles, you may have heard about how I did my day/night cycle and then how I added dynamic lighting on my building sprites. This first step was nice but it could use some improvements.
To summarise, I have a light source that travels across my world to shine light on the buildings from different angles throughout the day. Now there are a few issues:
Moreover, I would like to change how the sun and moon travel. Currently, my sun does this.
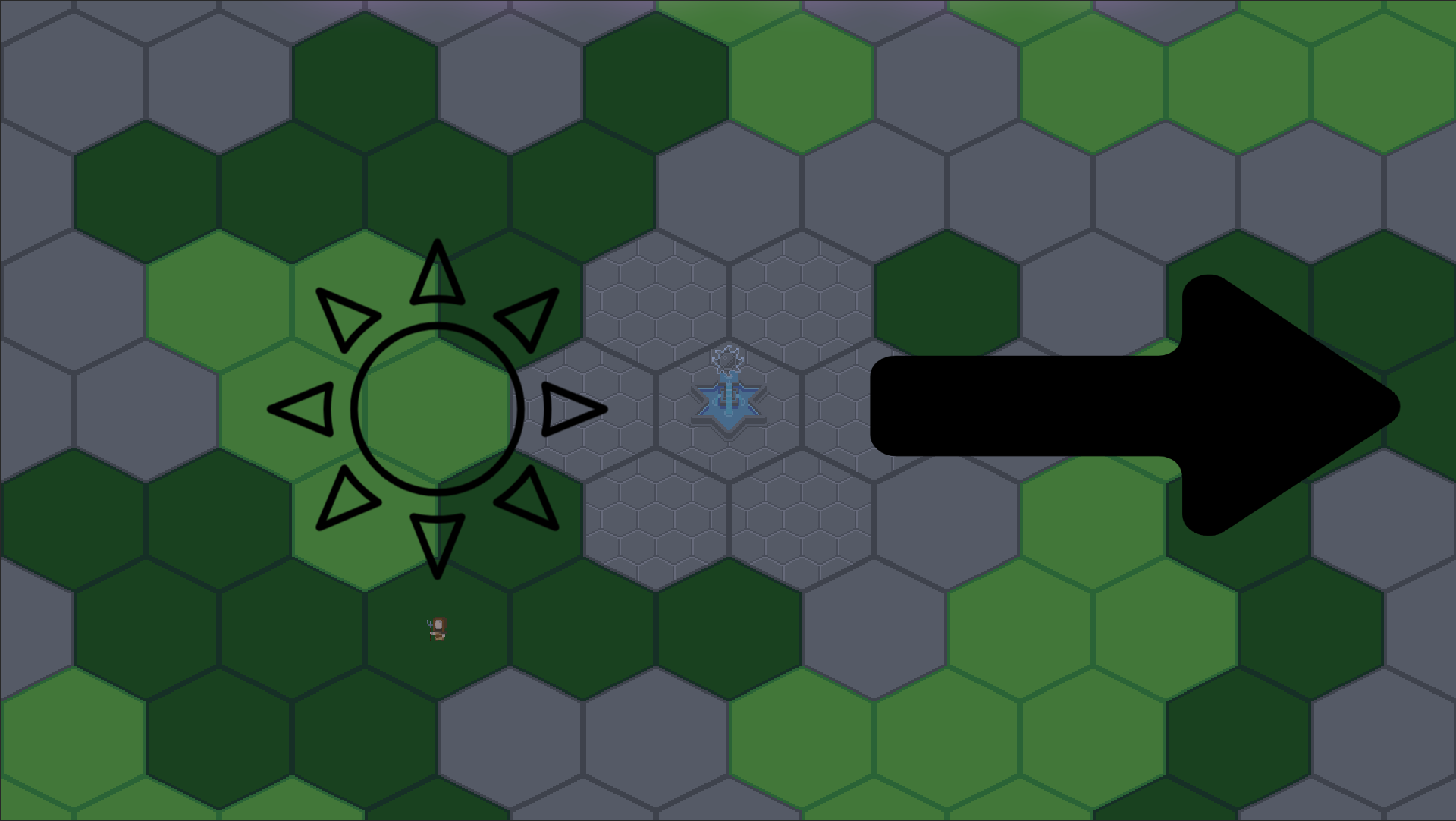
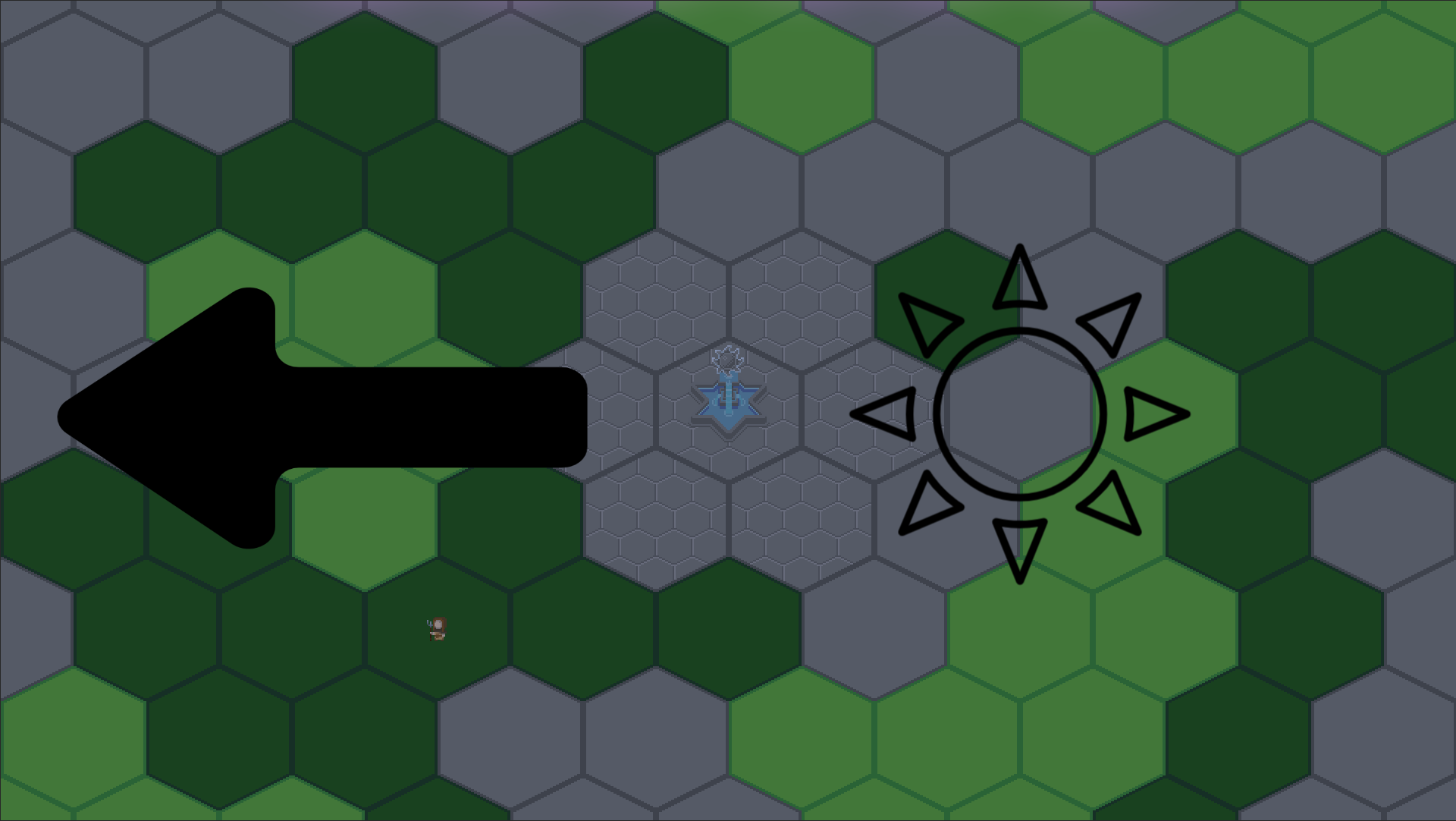
Or rather this, if I stop mistaking east for west.
And I would like it to do this
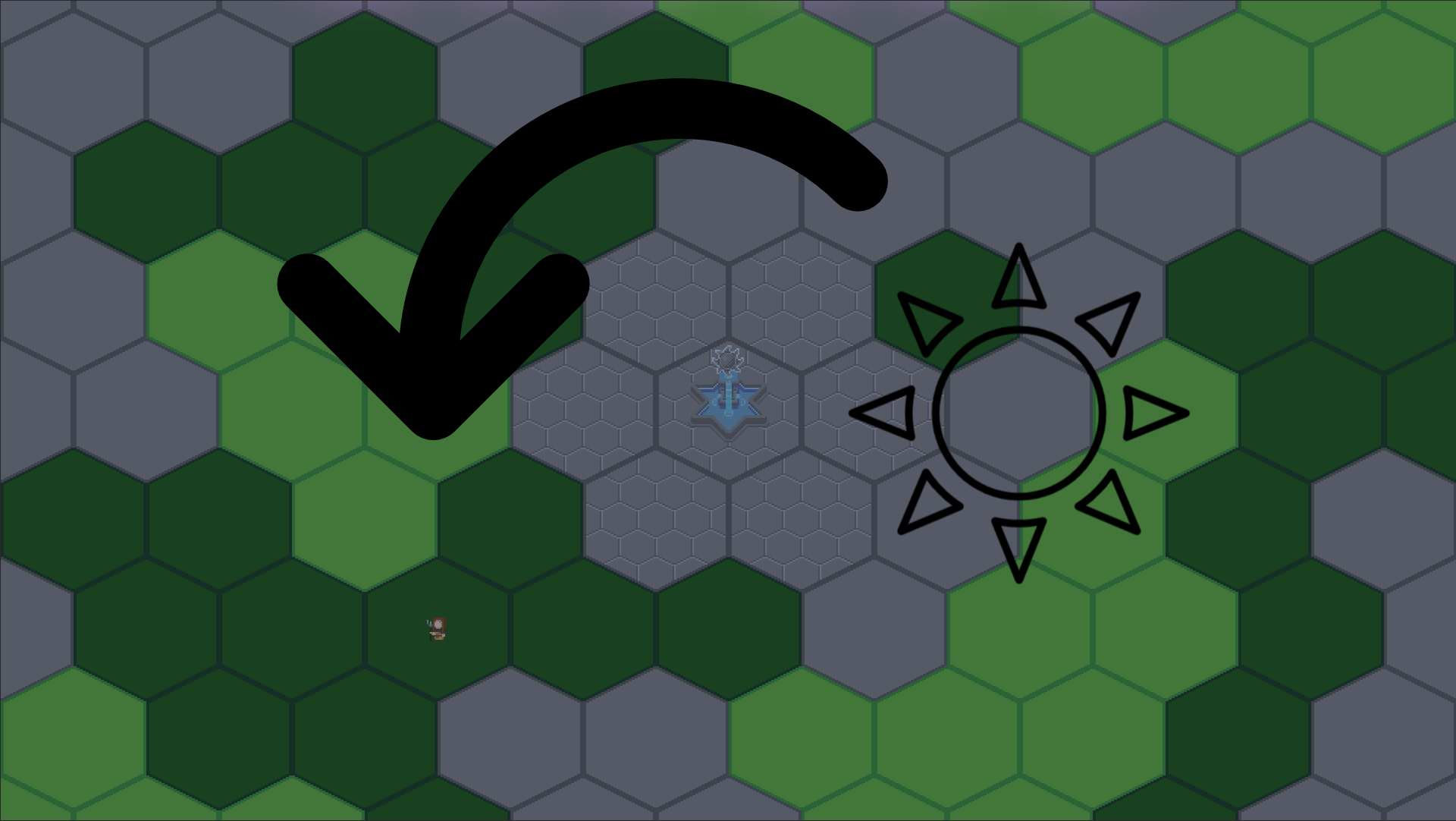
Let's see how I created a circular motion from a simple linear interpolation: in simpler terms, turn a number ranging from 0 to 1 at a constant pace into a perfect circular motion!
But first off, I need to make some adjustments. As mentioned before, let's fix the sun going east and add a moon. That allowed me to do some factoring in my code which is now way cleaner! I love it!

Yet, the buildings are still over-exposed to the light source when it travels above them. This is why we need to switch the trajectory of the light sources.
What are the elements we need to work with? Currently, the system is dead simple. My sun goes from an eastern point to a western point in a day. So we have two position vectors and a duration. In the end, we merely move the light source along a linear interpolation between the two positions. Do not be puzzled by the term "linear interpolation". This just describes a function which returns the position between two points at a given progress ratio.
For example, if we interpolate between the vectors (0,0) and (2,2), we would have the following values :
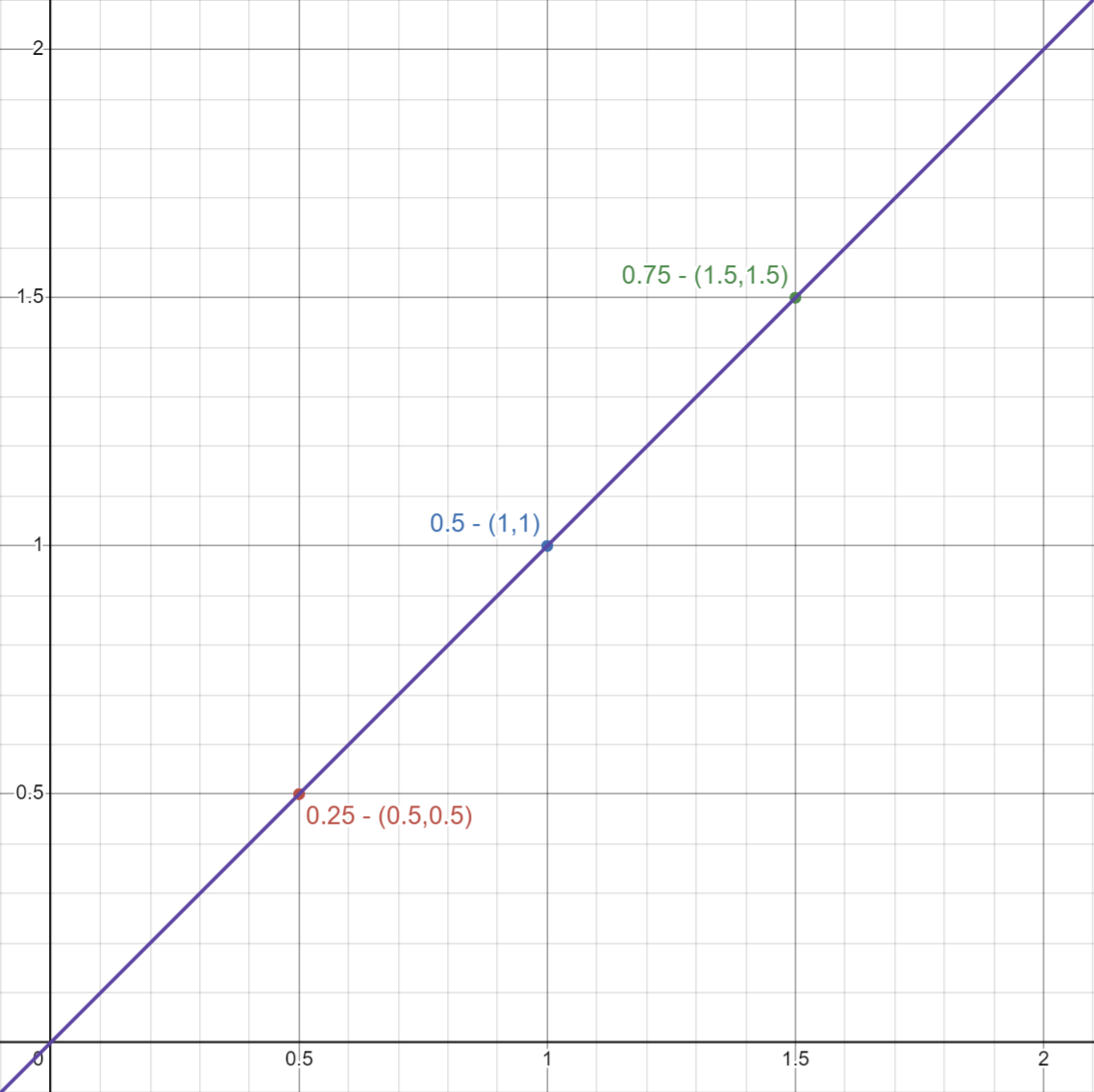
Now, you can imagine that if this progress rate is related to time the interpolation will describe a movement. So if my progress is the time of day divided by the total time of day, my interpolation will return the position of the sun throughout the day.
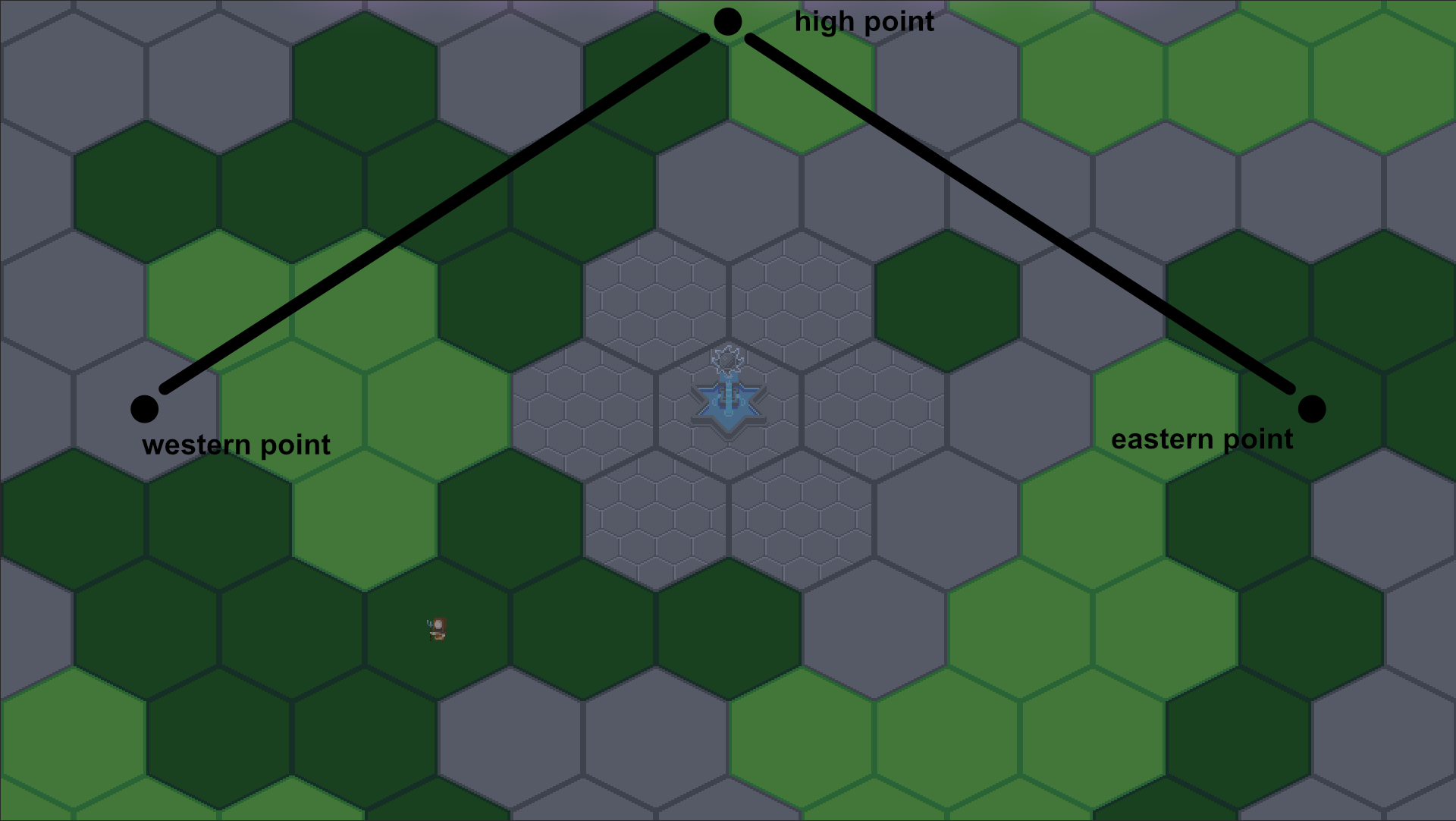
That is what we start with, but we want to change things up. As the movement is not solely on the horizontal (x) axis anymore we will need to store the position of the highest point on the vertical (y) axis.
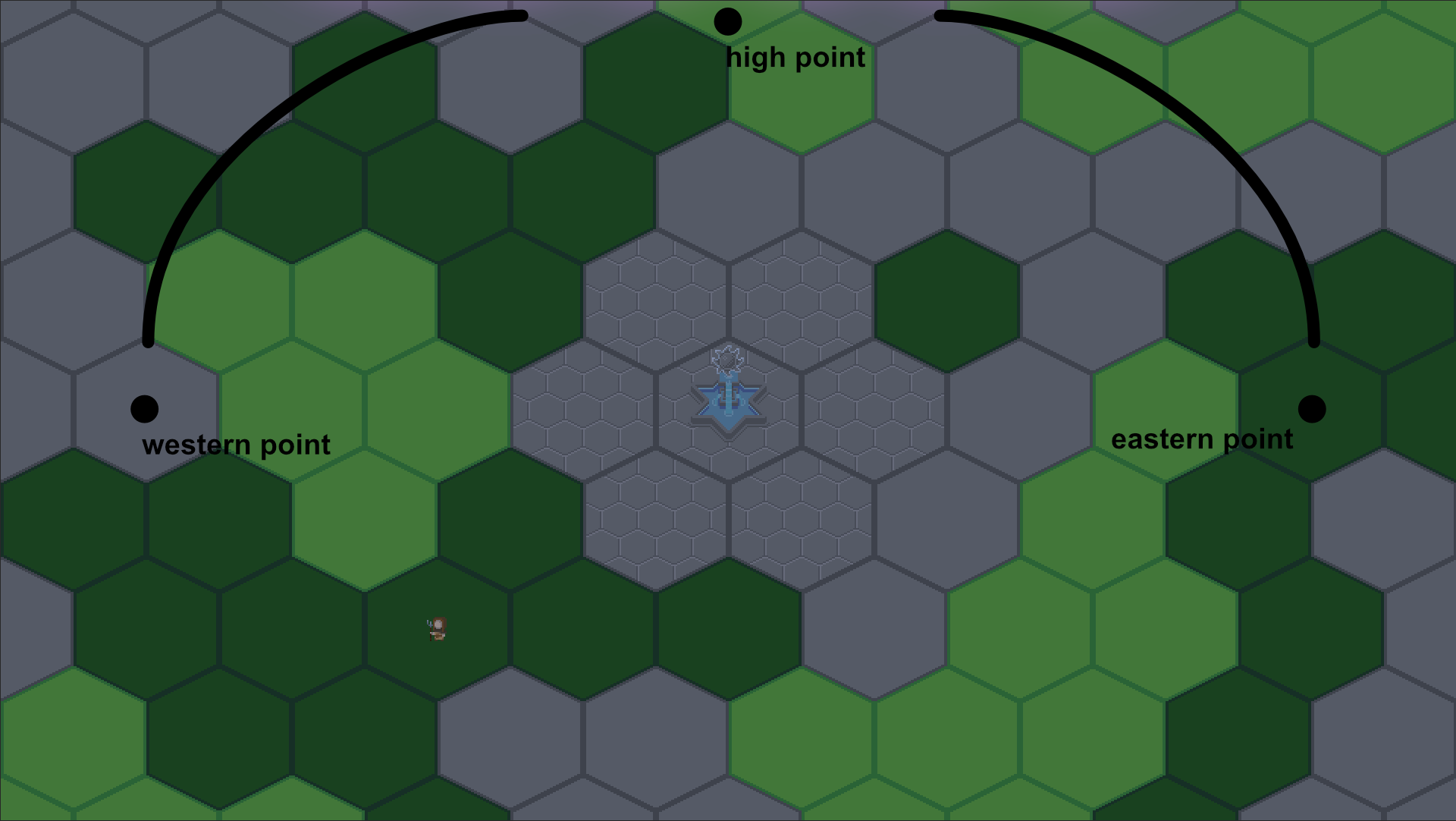
I first thought about storing a third position vector for the high point but when working with circular motion, it is way easier to work with a center point and a radius. So let's ditch the position vectors and go with that.
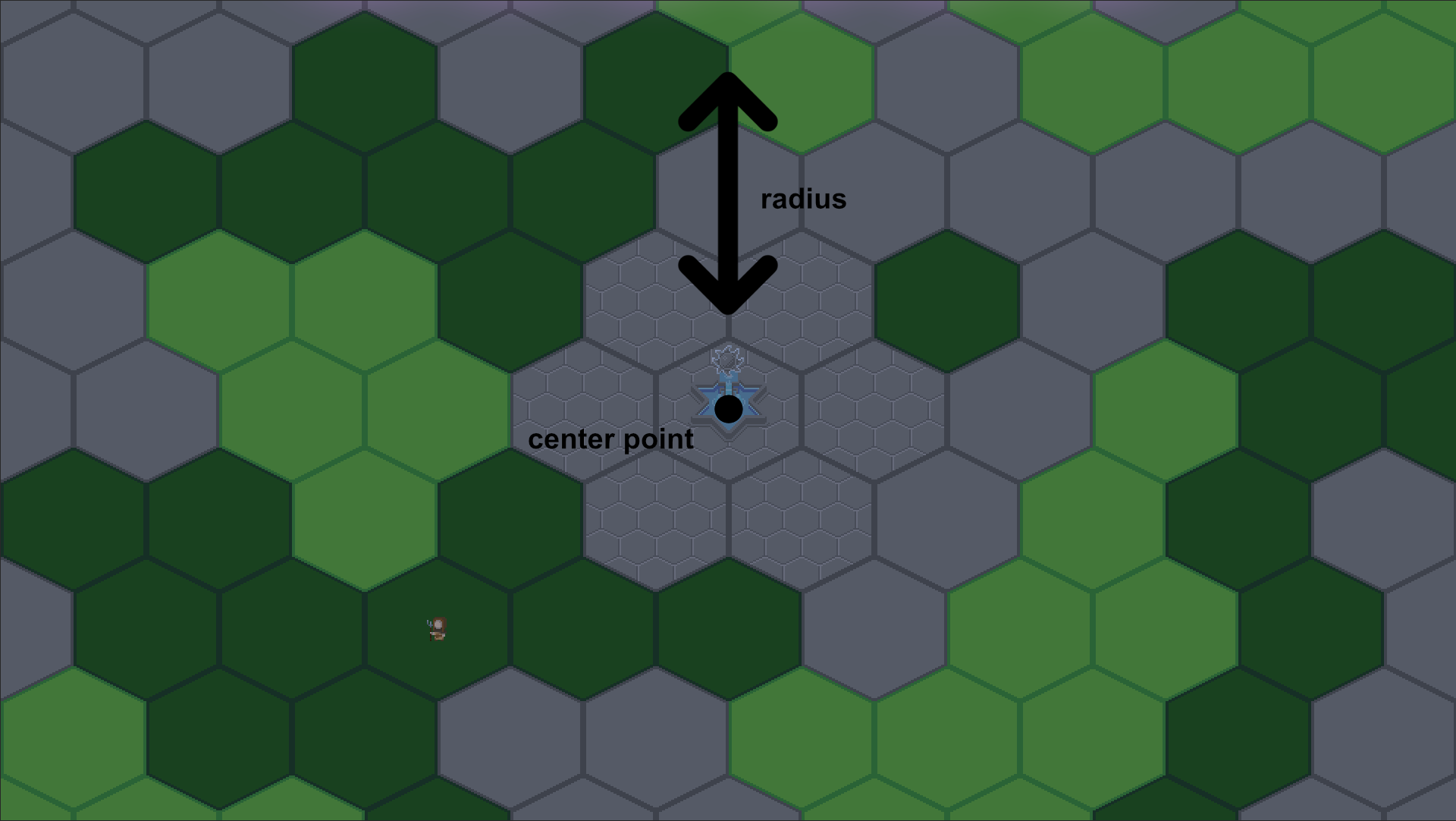
Now we will need to split our motion in two: the motion along the x-axis, and the motion along the y-axis. For the x, it remains pretty much the same. Okay, the sun will go up and down, but really, when you look only at the horizontal motion, the sun still goes east to west. Bear that in mind, because there is a detail we will need to come back to later. For the y-axis, the motion is not so obvious: it goes up and then goes down.
This is a periodic movement so we will need a sin function somewhere (or a cos; they are essentially the same thing). Sin() is great because at 0 it returns 0 and at PI it returns 0 as well. So if we take our progress rate and multiply it by PI the result will be bound to [0, Pi] rather than [0, 1]. We should then be able to feed it to our sin function to get our vertical movement.
1t being the progress ratio bound to [0, 1]
2y(t) = sin(t * Pi) ->Mmmmmh, close but not quite.
You see, the sinus function evolves between [0,1] so, in the middle of the movement, at a progress ratio of 0.5 (or Pi / 2 for our sin function) the sin function will return 1. So we need to multiply the whole thing by our radius. And as a last detail, because our function now evolves between [0, radius], we need to add the y value of the center point if it is not null.
1y(t) = centerPoint.y + sin(t * Pi) * radius
2x(t) = Mathf.Lerp(easternPoint.x, westernPoint.x, phaseProgres)And here’s the result:
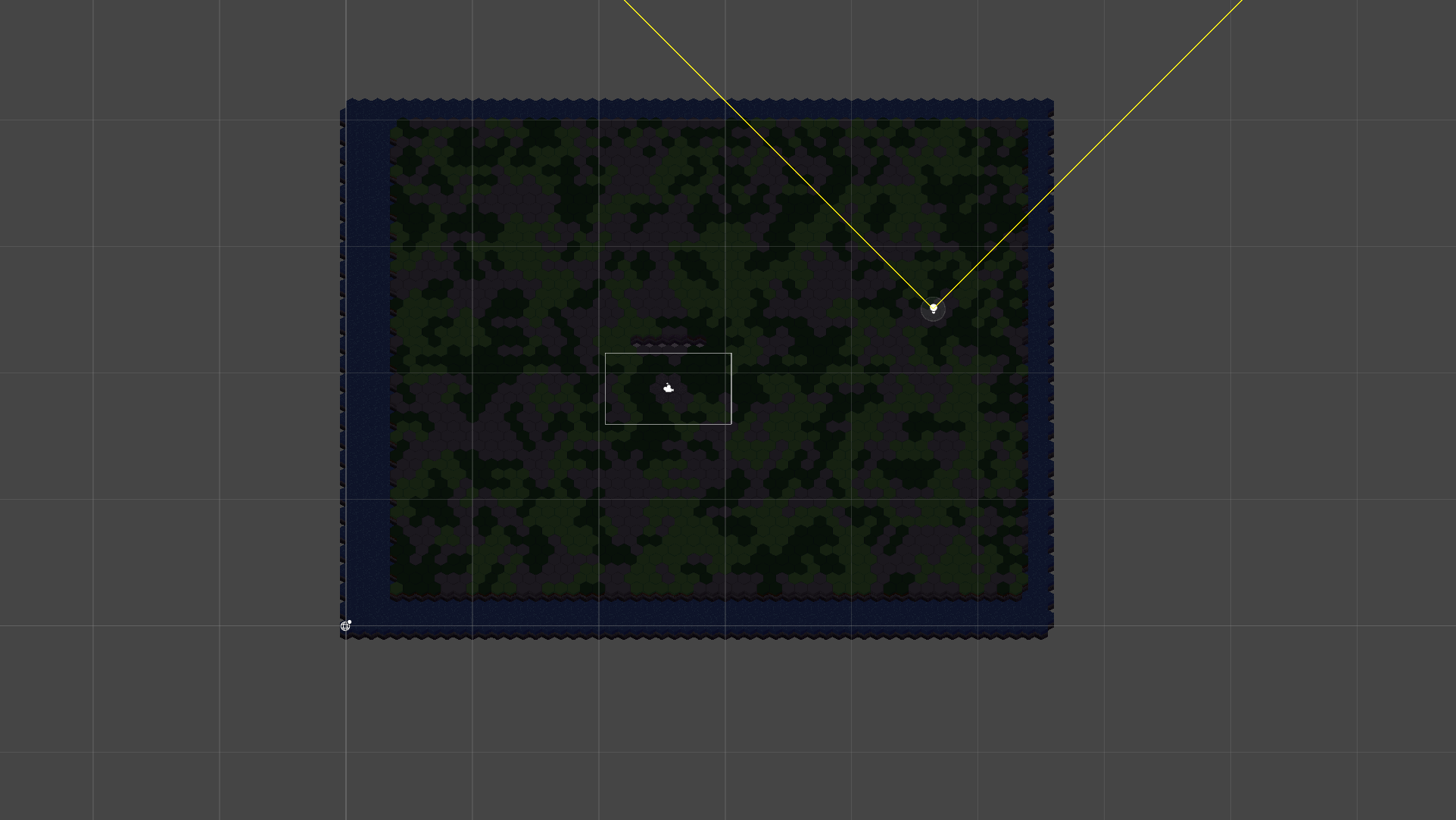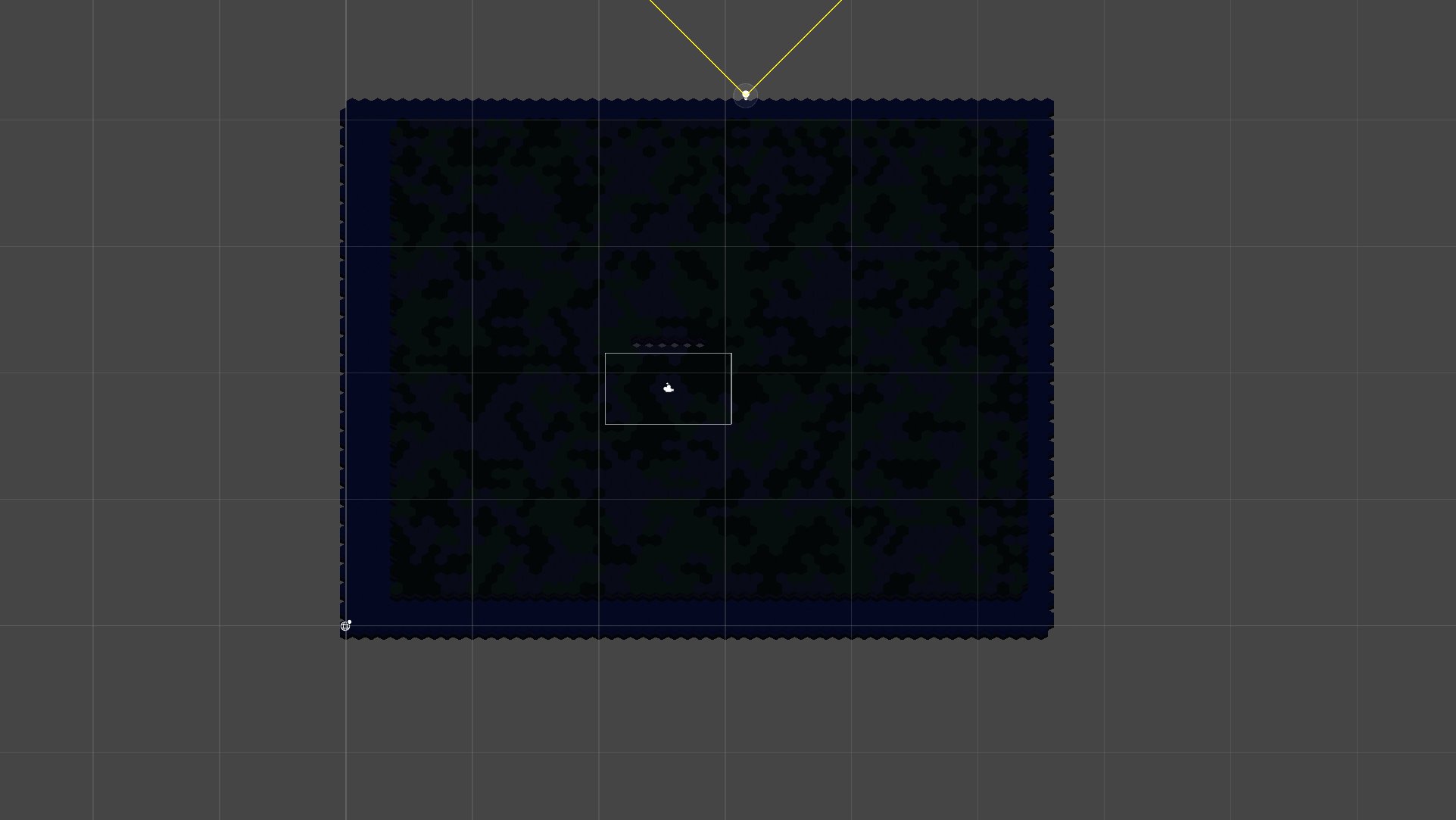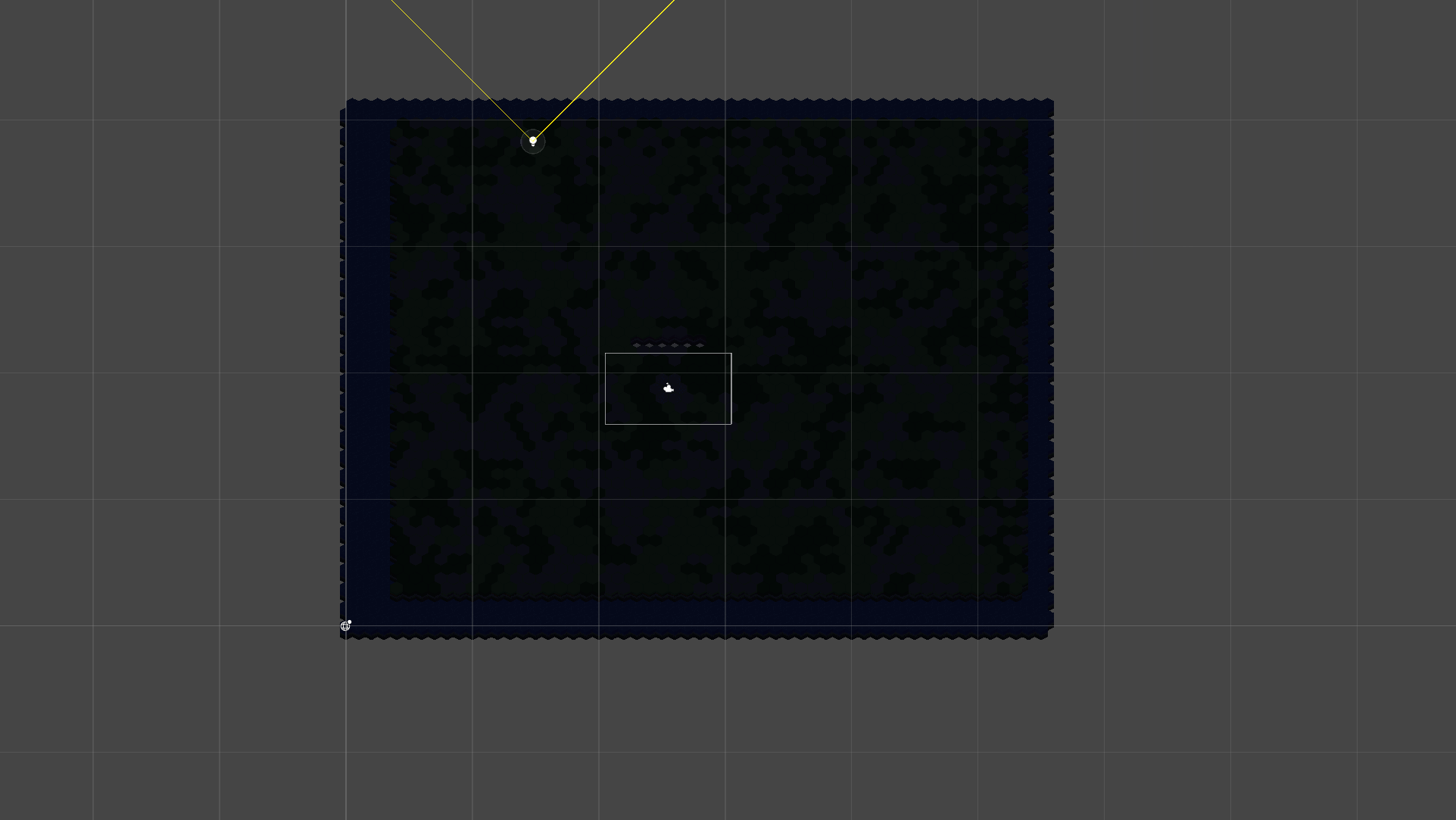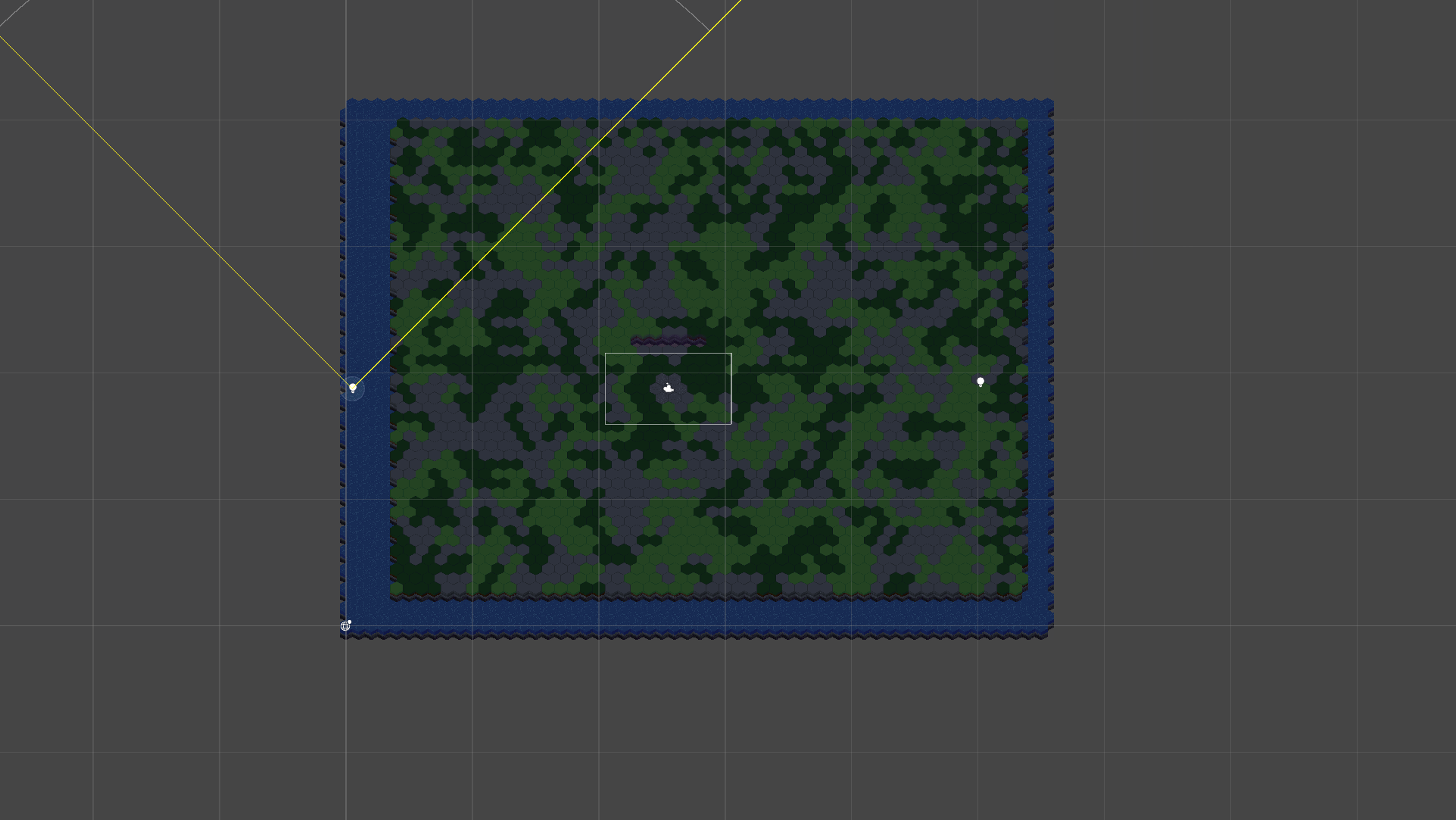
There is clearly an issue because the sun follows this trajectory.
We are close to a circular trajectory though. Remember the detail I said I would come back to? Now is the time 😀. You see, the issue lies with the way the position of the sun evolves on the x-axis. It is not in the values, because we want our sun to take this path. But it is rather in its speed along the x-axis. To trace a proper circle, the sun should be faster in the center and slower towards the end and the beginning. And it is exactly the behavior of a sin curve on [-Pi/2, Pi/2]: slow at the start, fast in the middle, and slow when reaching the top.
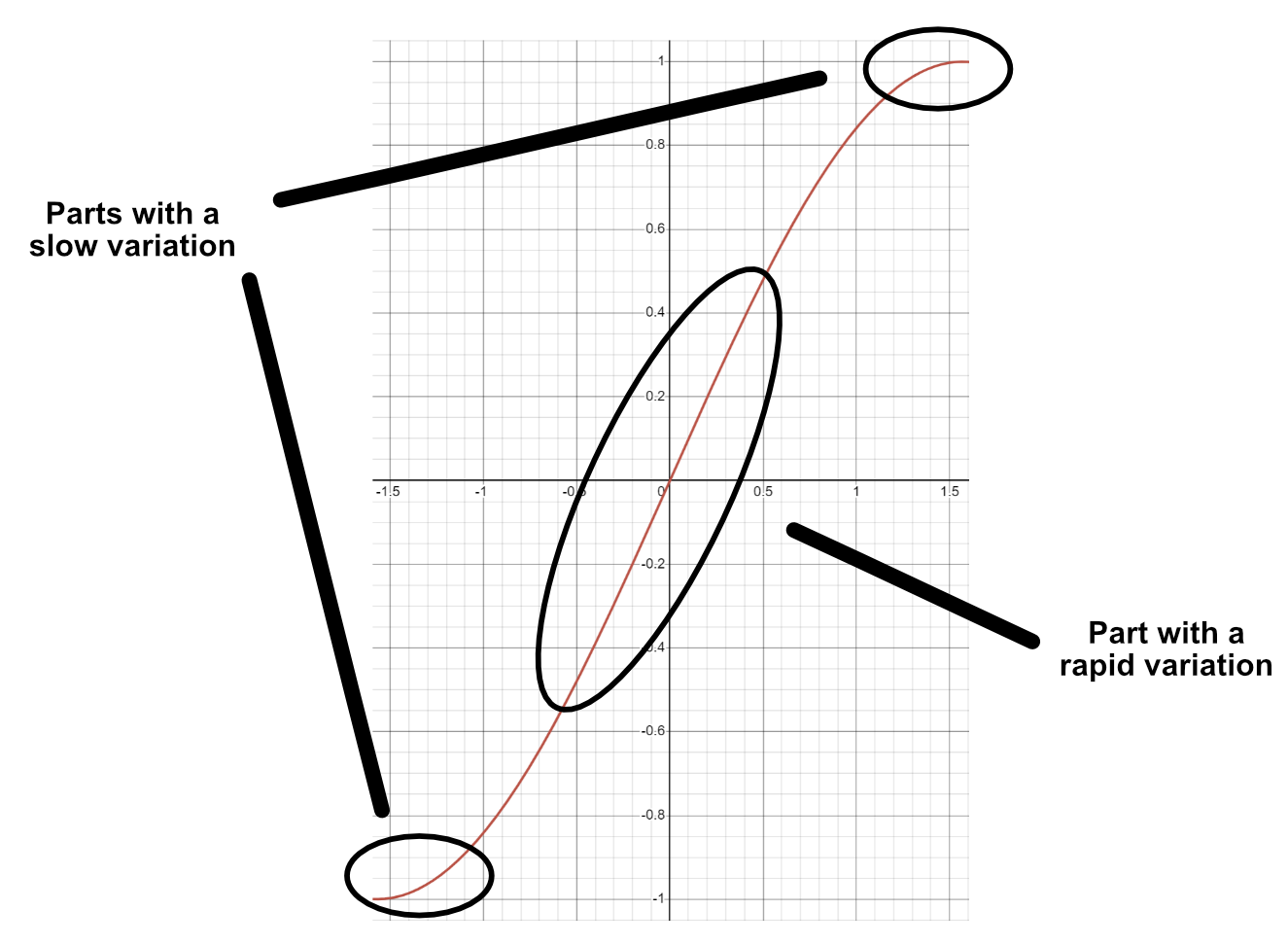
So before serving the progressRate to the formula for the horizontal movement, we need to smoothen it with a sin function. Our progress rate is bound to [0, 1]. So smoothRate = sin(progressRate * Pi) will return something bound to [0, 1] as well. But, it will not be monotonous because sin is increasing on [0, Pi/2] and decreasing on [Pi/2, Pi]. As such, we need to shift the part of the function we use: rather than using progressRate * Pi we can use (progressRate * Pi) - Pi/2.
However, our function now goes evolves in [-1,1]. So we need to shift that as well. To do so, we can add 1 to the total, making the function evolve in [0,2] and then divide it by 2 to remain bound in [0,1]. In the end, the function smoothing our progressRate is
1smoothRate = [sin((progressRate * Pi) - Pi/2) + 1] / 2
2y = centerPoint.y + sin(progressRate * Pi) * radius
3x = Mathf.Lerp(easternPoint.x, westernPoint.x, smoothRate)And now, the movement is perfectly circular!

Finally, as a last change, I want to switch for a round light source to a conic spotlight. Then, I need to rotate my light source during the movement so it always faces the center of the world. Because the light source starts at the eastern point and faces the center, it is at an angle of -90° at the start. By the end of the movement, it will have to face the opposite way, so we have an angle of 90°. This requires a simple linear function: angle = -90 + 180 * progressRate.

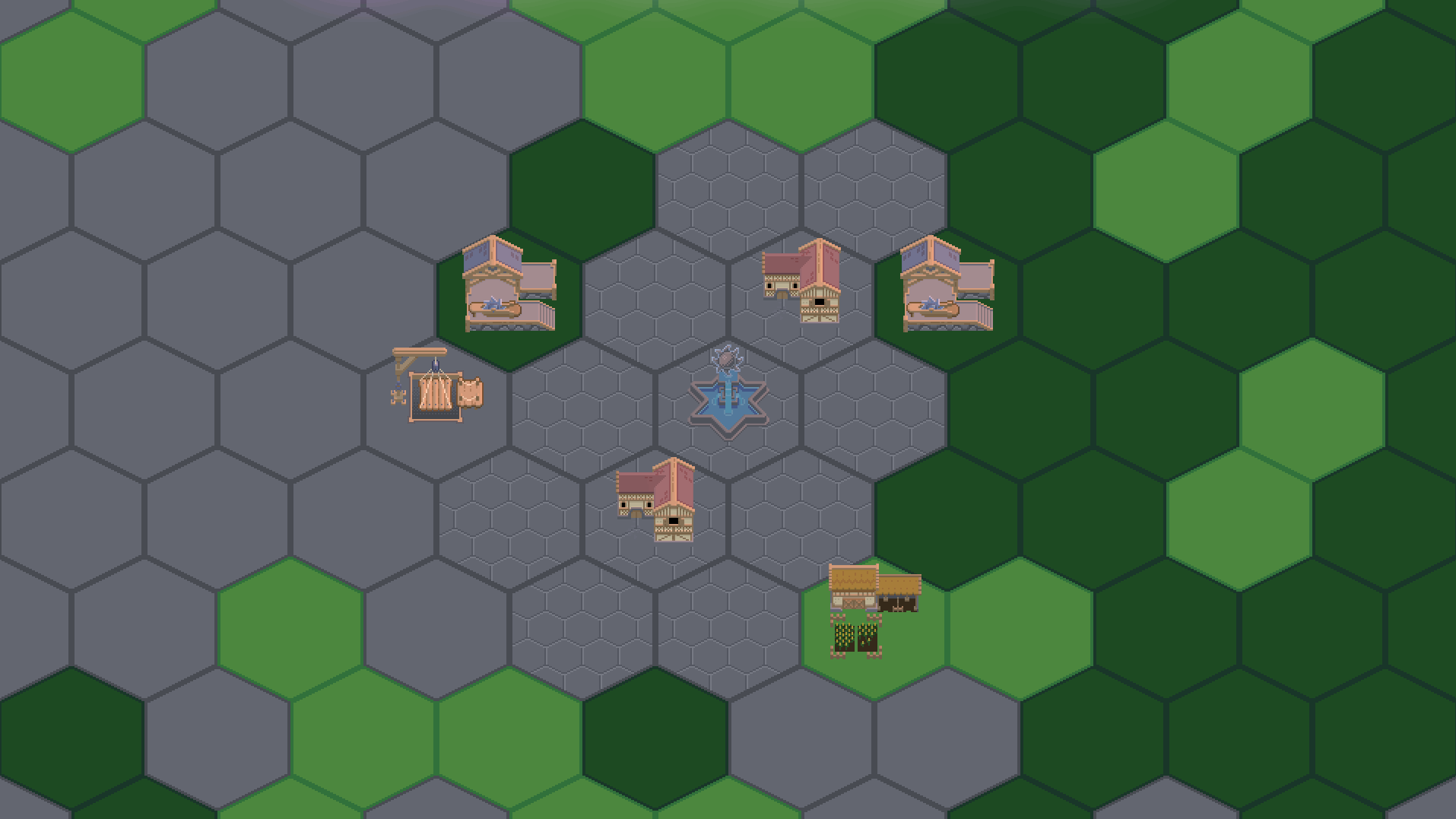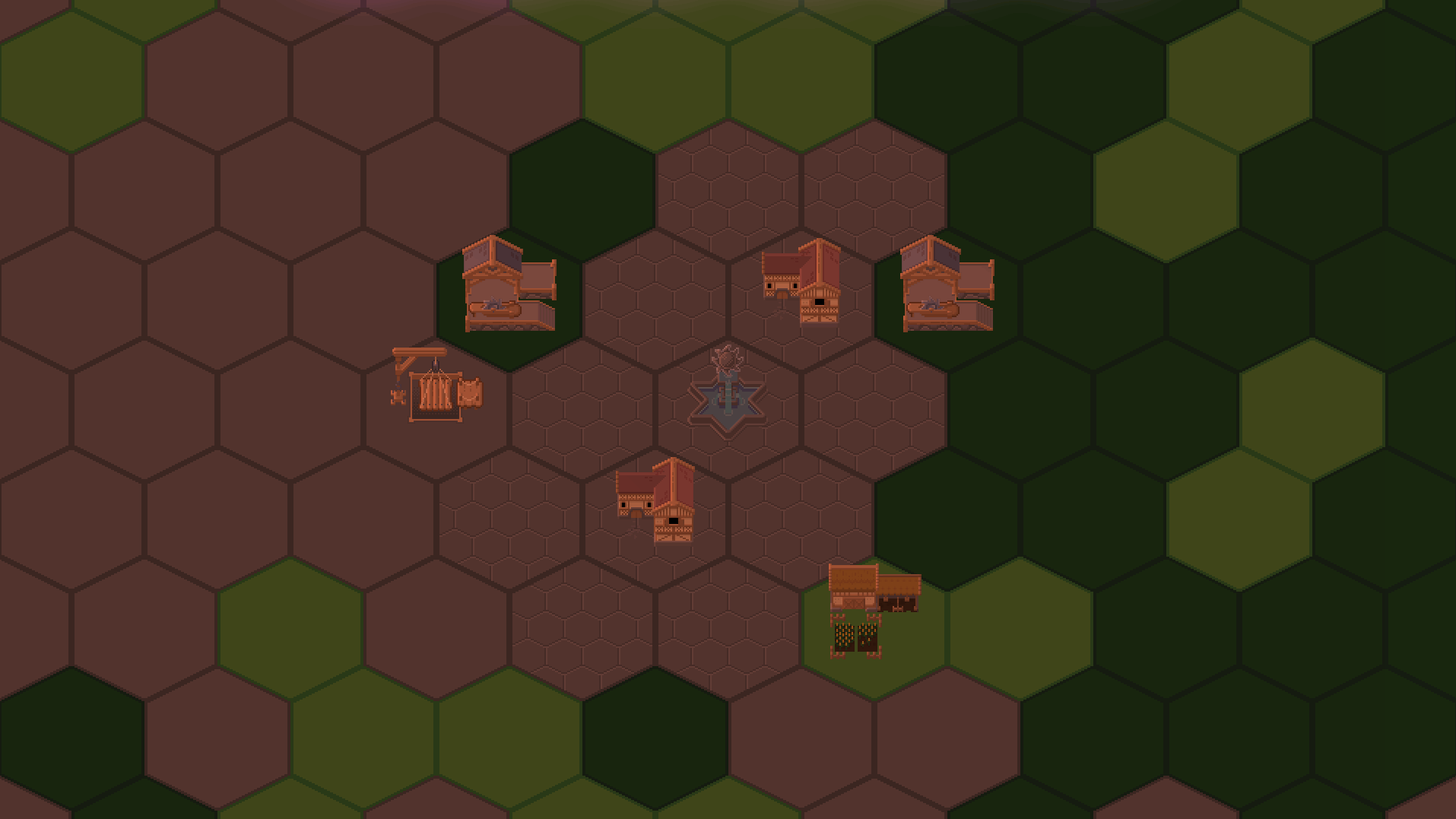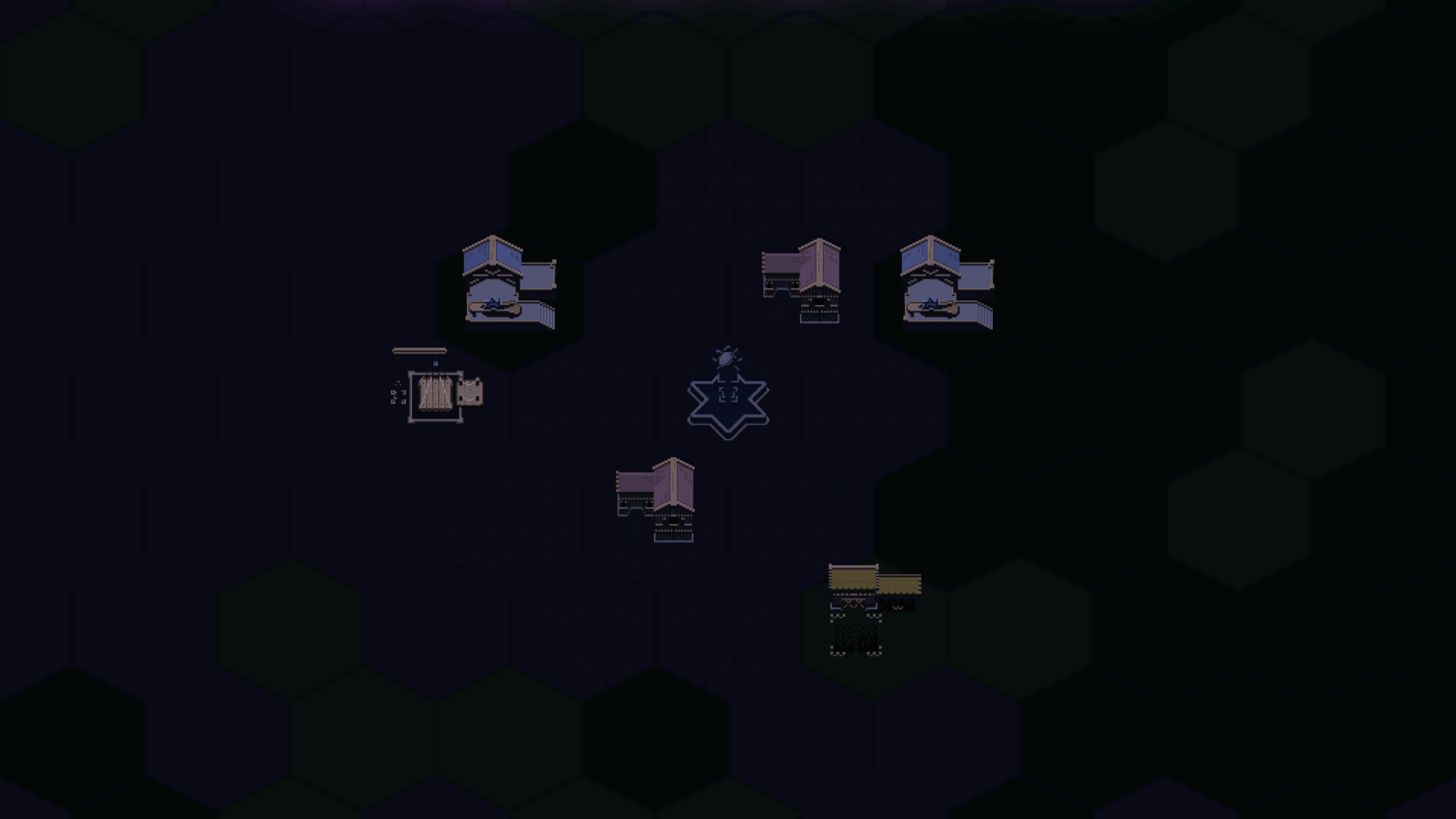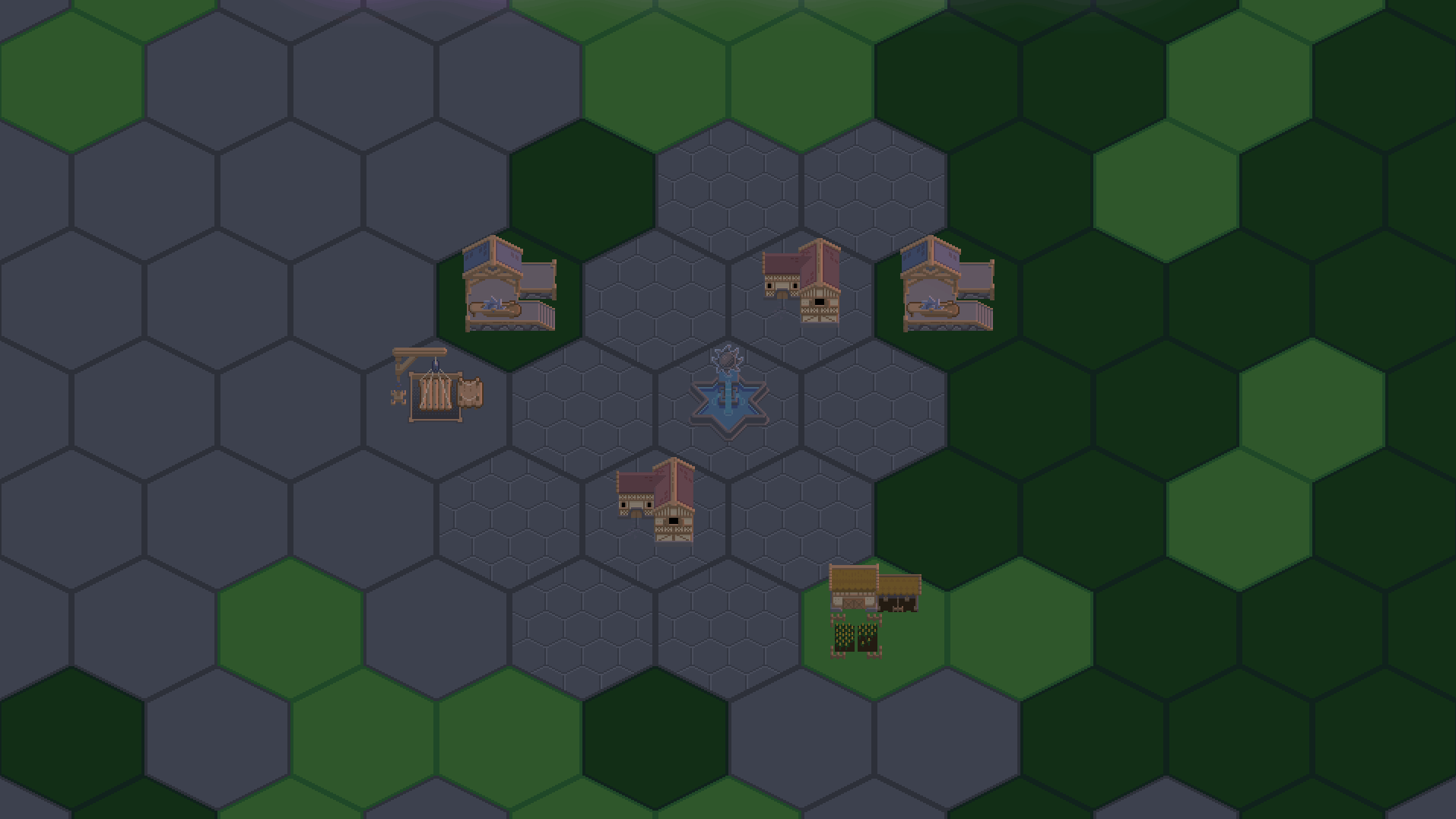
I hope you like the result! This article was a quite long and math-heavy but congratulations and thank you for reading to the end. Do not hesitate to message me if you have any questions! I hope to see you in the next post. 🦦